Binary Classificiation

(64 x 64 pixel)
위와 같은 사진을 input으로 넣었을 때, output으로 이 사진이 고양이인지 아닌지를 알고자 한다. (고양이이면 1, 아니면 0)
위의 사진이 컴퓨터에서는 어떻게 표현이 되는지 살펴보자.
사진을 저장하기 위해서는 컴퓨터는 3가지의 분리된 matric를 저장한다. 이는 RGB(red, green, blue)이며 color channel이다. 위의 사진이 64x64 pixel이므로 각각의 channel도 64x64이다.
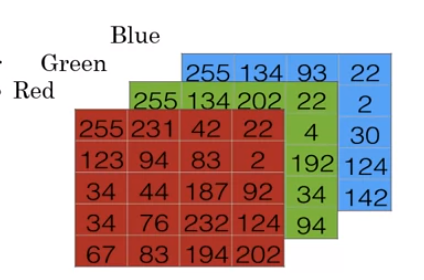
각각은 0에서 255 값을 가지며 검은색에 가까울 수록 0에 가깝고, 흰색에 가까울 수록 255에 가깝다. 이를 pixel intensity(희소 강도)라고 하는데, 이러한 값을 feature vector로 unroll하기 위해 feature vector x를 정의해야 한다. 이는 다음과 같이 각각의 pixel intensity value를 하나의 열행렬 vector로 flattening 할 수 있다. x = [ 255; 231; 42; 22; ... ;142] 이고, size는 64x64x3 = 12288(n_x) 이다.
이를 training에 사용해보자.
(x, y) 로 표현하며 x는 R^(n_x)의 원소이고, y는 {0, 1}의 원소이다.
m training examples : {(x(1), y(1)), (x(2), y(2)), ..., (x(m), y(m)} 이고, 이를 다시 X = [x(1), x(2), x(3), ..., x(m)] 으로 표현할 수 있다. 이는 (n_x) x m 행렬이다. 또한, Y = [y(1), y(2), ..., y(m)] 으로 표현할 수 있고, 이는 1 x m 행렬이다.
Logistic Regression
parameter가 2개가 주어지고, w는 IR(n_x)의 원소, b는 IR의 원소이다. 이를 통해 output ŷ 를 예측하고자 한다. 다음과 같이 표현할 수 있다. 여기서 T는 전치행렬을 의미하고, ŷ 는 P(y=1 | x) 이다.
ŷ = w^T * x + b
P(y=1 | x) 값이 0에서 1사이지만, 위의 식에서 ŷ 값은 1보다 크거나 음수가 될 수 있기 때문에 아래와 같이 sigmoid 함수를 적용한다.
ŷ = σ(w^T * x + b)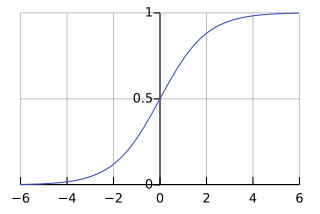
우리가 예측한 ŷ 과 실제 값 y의 차이를 Loss(error)라고 하고 이 값이 작도록 하는 것이 목표이다. Loss function은 다양한 종류가 있는데 여기서는 2가지만 살펴보고자 한다.
- 평균제곱오차(MSE) : L(ŷ, y) = 1/2 * ( ŷ - y )^2
- 로그 오차(LE) : L(ŷ, y) = -(y * log ŷ + (1-y) log (1- ŷ))
- if y=1 : L(ŷ, y) = - log ŷ // log ŷ 값이 커지길 원하므로 ŷ 값이 커지길 원한다.
- if y=0 : L(ŷ, y) = -log(1- ŷ) // log (1- ŷ ) 값이 커지길 원하므로, ŷ 값이 작길 원한다.
Loss function은 하나의 sample에 대한 오차 값이였다면 Cost function 은 training set에 대한 오차 값의 평균이다. 여기서 파라미터 w와 b가 training set에서 얼마나 잘 진행되고 있는지를 측정한다. 이는 다음과 같이 표기한다.
J(w, b) = 1 / m * Σ L(ŷ, y)
Gradient Descent
앞서 언급한 cost function 을 최소화하는 파라미터 w, b를 찾고자 한다.
J(w,b)를 3차원 그래프에 표현하면 다음과 같다. (convex)
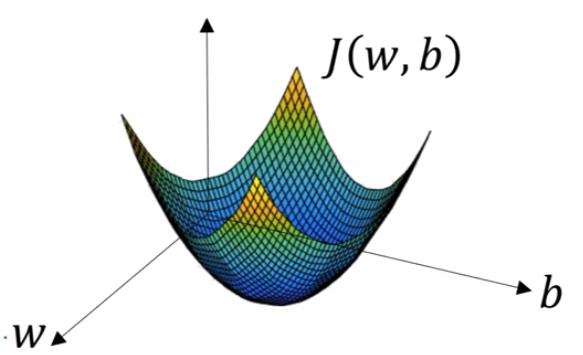
참고로, non convex에서는 많은 local optimal이 존재할 수 있다.
쉽게 그림으로 그리기 위해서 b를 무시하고 생각해보자.
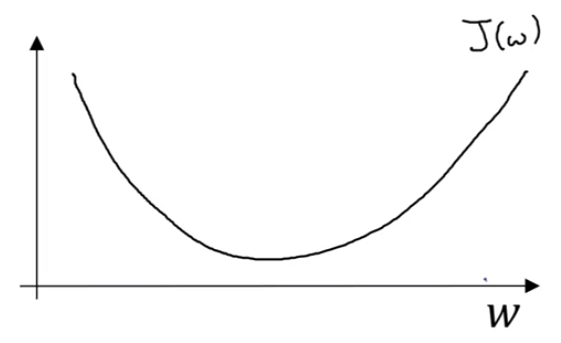
Repeat until convergence { w := w - α * dJ(w)/dw }
요약하자면, 기울기가 양수일때는 w를 왼쪽으로 옮기고, 기울기가 음수일 때는 오른쪽으로 옮긴다. 또한, 기울기의 절댓값이 큰 경우에는 빠르게 이동하고, 작은 경우에는 느리게 이동한다. 여기서, α 는 learning rate(학습률)이고, 초기 위치는 임의의 값이다.
이제, 같은 논리로 J(w,b)를 생각해보자.
Repeat until convergence {w:= w-α * dJ(w,b)/dw}
{b:= b-α * dJ(w,b)/db}
이를 아래와 같이 합쳐서 partial derivative(편미분) 으로 표기한다.
repeat until convergence { w := w - α * ∂J(w,b)/∂w }
- Computation Graph 예제
J(a,b,c) = 3(a+bc)
u = b*c
v = a+u
J = 3v
a = 5, b=3, c=2 과 같이 input이 주어질 때, 다음과 같이 계산된다.
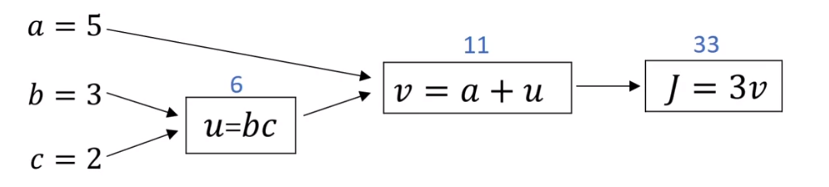
그 다음으로는 derivative를 계산하기 위해서 반대 방향(back propagation)으로 계산된다.
우리가 알고자 하는 것은 앞서 언급했던 dJ/dw 이므로 dJ/da, dJ/db, dJ/dc 값이다.
dJ/dv = 3
dJ/da = dJ/dv * dv/da = 3 * 1 = 3
dJ/db = dJ/dv * dv/du * du/db = 3 * 1 * c = 6
dJ/dc = dJ/dv * dv/du * du/dc = 3 * 1 * b = 9
이제, Logistic regression에서 gradient descent를 살펴보자.
z = w^T * x + b
ŷ = a = σ(z)
L(a, y) = -(ylog(a) + (1-y)log(1-a))
loss를 줄이기 위해 parameter(w,b)를 변경하고자 한다.
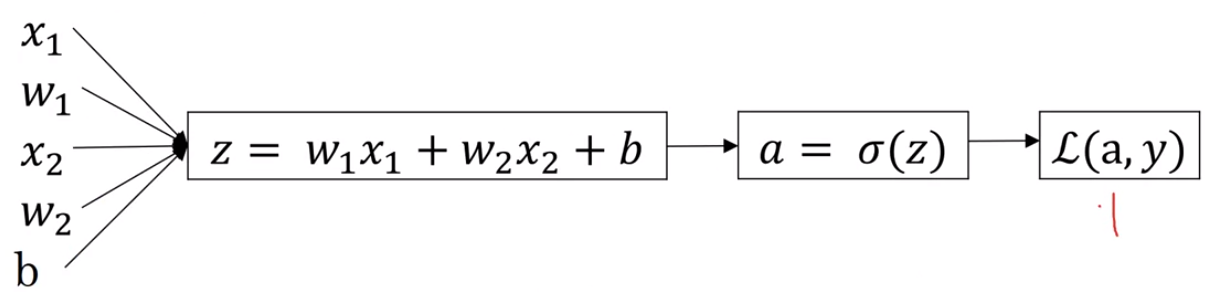
구해야 하는 derivative 값은 다음과 같다.
dL/dw1 = dL/da * da/dz * dz/dw1 = dL/da * da/dz * x1
dL/dw2 = dL/da * da/dz * dz/dw2 = dL/da * da/dz * x2
dL/db = dL/da * da/dz * dz/db = dL/dz * 1 = dL/da * da/dz
여기서 dL/da * da/dz 즉, dL/dz 가 겹치므로 구해보자.
dL(a,y)/da = -y/a + (1-y)/(1-a)
dL(a,y)/dz = dL(a,y)/da * da/dz = dL(a,y)/da * a(1-a) = -y(1-a)+ a(1-y) = a-y
위의 da/dz를 구하기 위해 sigmoid 함수의 도함수를 알아야 한다.
구체적인 도함수 계산 과정은 아래 링크에 다.
http://taewan.kim/post/sigmoid_diff/
σ'(z) = σ(z)*(1-σ(z))
따라서, derivative는 다음과 같다.
dL/dw1 = x1 * (a-y)
dL/dw2 = x2 * (a-y)
dL/db = a-y
이제, 위의 결과를 바탕으로 m training examples의 Logistic regression에서 gradient descent를 python 코드로 살펴보자.
J=dw1=dw2=db=0
for i in range m:
z(i) = w^T * x + b
a(i) = σ(z(i))
J+=-(y(i)log a(i) + (1-y(i))log(1-a(i)))
dz(i) = a(i) - y(i)
dw1 += x1(i) * dz(i)
dw2 += x2(i) * dz(i)
db += dz(i)
J /= m
dw1 /= m
dw2 /= m
db /= m
위의 코드를 거쳐서 w1,w2,b가 아래와 같이 업데이트 된다.
w1 := w1 - α*dw1
w2 := w2 - α*dw2
b := b - α*db
추가로, input unit이 n개라고 하면 x1,w1,x2,w2, ..., xn, wn, b로 설정되며 이에 맞게 코드를 구현할 수 있다.
또한, 이를 벡터화해서 다음과 같이 구현할 수 있다.
Z = np.dot(np.transpose(w), X) + b
A = σ(Z)
dz = A-Y
dw = 1/m * np.transpose(Z)
db = 1/m * np.sum(dz)
w -= α * dw
b -= α * db
'연구실 > 인공지능(Coursera)' 카테고리의 다른 글
| [AI 6주차] Optimization Algorithm (0) | 2024.07.15 |
|---|---|
| [AI 5주차] Deep learning의 실용적인 측면 (0) | 2024.07.02 |
| [AI 4주차] DNN(깊은 신경망) (0) | 2024.06.27 |
| [AI 3주차] Swallow Neural Network(얕은 신경망) (1) | 2024.06.27 |
| [AI 1주차] Deep Learning 소개 (0) | 2024.06.25 |



