Swallow Neural Network(얕은 신경망)
: hidden layer가 하나만 존재하는 Neural Network를 의미한다.
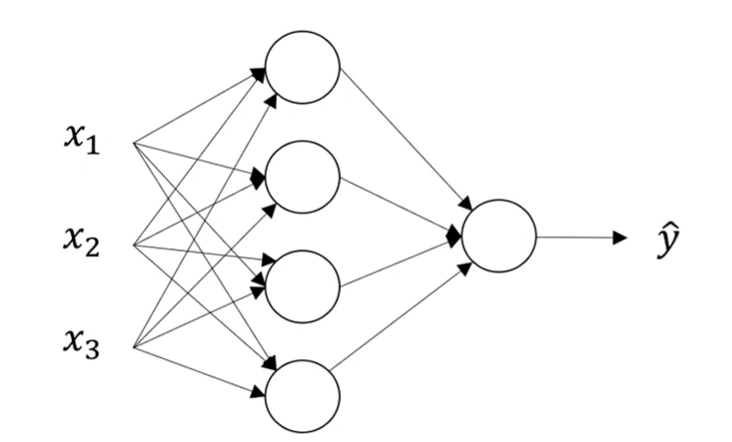
input layer hidden layer output layer predicted value
a^[0] = X a^[1] a^[2] ŷ = a
시작하는 위치에 있는 x1, x2, x3는 input value이고 마지막에 있는 ŷ은 output value이다. input value가 있는 층을 input layer, output value가 return되는 마지막 노드를 output layer, 그리고 그 사이의 layer를 hidden layer라고 한다.
일반적인 신경망에서 각각의 노드는 다음 layer의 노드와 모두 연결되어 있다. 이를 fully connected라고 한다.
얕은 신경망에서 input layer는 0번째 layer, hidden layer 1번째 layer, output layer는 2번째 layer이다. 이는 a^[0], a^[1], a^[2]로 표현하고 x1,x2,x3는 대문자 X, ŷ = a 로 표기할 수 있다.
신경망 process를 보면 input value가 hidden layer를 거쳐 output value ŷ 이 계산되는 과정이다. 여기서 ŷ 은 예측값이고, 이를 실제 값인 y와의 오차를 계산해서 이를 최소화하는 방향으로 업데이트 하는 과정으로 학습이 이루어진다.
이제, output을 어떻게 계산하는 지 살펴보자.
앞서 logistic regression을 살펴봤었다.이는 linear regression에서 logistic function을 적용한 것이다. 이는 가중치 벡터 w와 입력 벡터 x를 내적(w^T*x)하고 bias 를 더하고, sigmoid 함수를 거쳐서 output이 계산된다.

weight와 bias에 대한 설명 : https://jh2021.tistory.com/3

하지만, python으로 구현할 때 위와 같이 반복문으로 구현하면 비효율적이므로 벡터로 표현해보자.
input layer의 [x1 ; x2 ; x3] 를 x라고 하자. 이는 3 x 1 행렬이다.
output layer의 [ z1^[1] ; z2^[1] ; z3^[1] ; z4^[1] ] 을 z^[1]이라고 하자. 이는 4 x 1 행렬이다.
[ b1^[1] ; b2^[1] ; b3^[1] ; b4^[1] ] 를 b^[1] 이라고 하자. 이는 4 x 1 행렬이다.
[ w1^[1]T ; w2^[1] ; w3^[1]T ; w3^[1]T ]를 W^[1]이라고 하자. 이는 4 x 3 행렬이다.
이를 아래와 같이 표현할 수 있다.

첫번째 수식을 보면, W^[1]은 4 x 3 행렬이고, x는 3 x 1 행렬이므로 곱했을 때, 4 x 1 행렬이 되며, b^[1] 도 마찬가지로 4 x 1 행렬이므로 더하면 4 x 1이 된다. 이는 z^[1] 행렬의 크기와 같다.
여기서, 세번째 수식을 보면 W^[2]는 1 x 4 행렬이고, a^[1]은 4 x 1 행렬이며 곱했을 때, 1 x 1 행렬이 된다. b^[2]도 마찬가지로 1 x 1 행렬이고 더했을 때, 1 x 1 행렬이 된다. 이는 우리가 최종적으로 구하고자 하는 z^[2] 의 크기와 같다. 이는 우리가 추정한 predicted value인 ŷ 이 된다.
m training examples에서 python 코드로 살펴보자.
for i=1 to m:
z^[1](i) = W^[1]*x(i) + b^[1]
a^[1](i) = σ(z^[1](i))
z^[2](i) = W^[2]*a^[1](i) + b^[2]
a^[2](i) = σ(z^[2](i))
여기서, 행렬 a의 수직 방향은 hidden units의 개수를 의미하며, 수평방향은 training example을 의미한다.
Activation function
: hidden layer에서 사용되는 함수이다. 앞서 봤던 sigmoid 함수가 이에 해당한다. 하지만 대부분의 경우에는 이 함수보다는 다른 함수가 더 효과적이다. hyperbolic tangent function(tanh)나 ReLu가 이에 해당한다. https://leeejihyun.tistory.com/32
아래는 tanh function graph이다.


하지만, z의 절댓값이 너무 크면 gradient가 0에 가까우므로 back propagation 과정에서 gradient descent 속도가 느려질 수 있다. 그리고 이후에 살펴볼 심층 신경망에서 layer가 많아지면 gradient vanishing problem이 발생할 수 있다. 즉, gradient가 update가 되지 않아 최적의 모델을 찾을 수 없다. 그래서 대안으로 ReLU function을 사용하기도 한다.
아래는 ReLu function의 graph이다.

하지만, 여전히 음수일 때는 gradient가 0이라는 단점이 있어서, leaky ReLu를 사용하기도 하지만, 실제로 잘 사용하지는 않는다.
앞서 본 activation function은 모두 non linear activation function이다. linear function을 쓰지 않는 이유는 다음과 같다.
z^[1] = w^[1]T * x + b^[1]
a^[1] = w^[2]T * z^[1] + b^[2]
= w^[1]T * w^[2]T * x + W^[1]T * b^[1] + b^[2]
= W'x + b'
이후에 살펴볼 DNN에서 여러 layer를 거쳐도 하나의 선형결합으로 표현이 되기 때문에 layer를 많이 쌓는 의미가 없다.그래서, 모델의 표현성을 높이고 더 많은 계산을 하기 위해 비선형 활성화 함수를 도입한다.
Gradient descent in Neural Network
forward propagation을 통해 ŷ 을 구하고, 이를 실제 값 y와의 오차(손실)을 통해 이를 최소화하는 방향으로 업데이트가 이루어진다고 했다.
https://whitehacking.tistory.com/42
[AI 2주차] 신경망 기초
Binary Classificiation(64 x 64 pixel)위와 같은 사진을 input으로 넣었을 때, output으로 이 사진이 고양이인지 아닌지를 알고자 한다. (고양이이면 1, 아니면 0) 위의 사진이 컴퓨터에서는 어떻게 표현이 되
whitehacking.tistory.com
앞서, cost function은 m개의 training examples에서 다음과 같이 표현할 수 있음을 알아봤다. (L은 ŷ 과 y의 오차함수)
J(W, b) = 1/m * Σ(i=1~m) L(ŷ , y)
m개의 training sample에서 각각의 Loss를 구하고 이들의 평균을 비용함수라고 했는데 이 값이 최소가 되도록 gradient distance를 통해 w, b를 업데이트 하고자 한다.
Repeat until convergence {w:= w-α * dJ(w,b)/dw}
{b:= b-α * dJ(w,b)/db}σ`(z) = σ(z)*(1-σ(z))
위의 내용을 바탕으로 얕은 신경망에서 dw와 db를 계산해보자.
Back propagation :
dz^[2] = A^[2] - y
dw^[2] = 1/m * A^[1]T * dz^[2]
db^[2] = 1/m * np.sum(dz^[2], axis=1, keepdims = True)
dz^[1] = w^[2]T * dz^[2] * g[1]`(z^[1])
dw^[1] = 1/m * dz^[1] * X^T
db^[1] = 1/m * np.sum(dz^[1])
각각의 layer에서 dw, db를 구했다. 이제 이를 바탕으로 update를 하면 ŷ과 y의 오차를 최소화하는 모델을 만들 수 있다.
Parameter Initailization
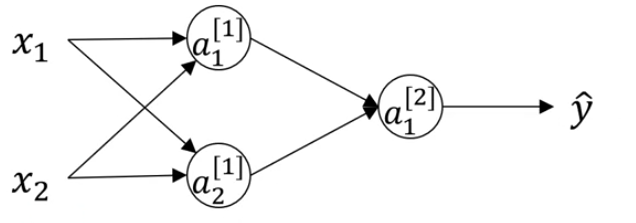
training 을 하기 전에 W와 b를 initialize하는 것은 중요하다.
W를 영벡터로 초기화할 경우 문제가 발생한다.
그림에서 보면 hidden layer에서 각 노드의 activation function은 같고 input node도 같기 때문에 a1^[1] 과 a2^[1] 값은 같아진다. 또한 back propagation 과정에서 dz1^[1] 과 dz2^[1]의 값도 같아진다. 즉, 모든 뉴런의 gradient가 같아지는 문제가 발생한다. 즉, weight를 업데이트 하지 못하므로 학습을 하지 못한다. 이를 network symmetric problem이라고 한다.
또한, weight가 균등하지 않으면, 특정 뉴런에 편향이 될 수 있으므로 다양한 탐색이 어려울 수 있다.
그래서 random하게 initialize해야 한다.
W^[1] = np.random.rand((2,2)) * 0.01
b^[1] = np.zero((2,1))
...
여기서 0.01을 곱한 이유는 weight의 값을 작게 만들기 위해서이다. z^[1] = w^[1] * x + b^[1] 에서 w가 크다면 z도 크므로 gradient가 0에 가깝기 때문에 학습이 매우 느려진다.
참고로, b는 random하게 initialize된 weight로 인해 network symmetric problem이 해결이 되므로 영벡터로 초기화해도 문제가 되지 않는다.
'연구실 > 인공지능(Coursera)' 카테고리의 다른 글
| [AI 6주차] Optimization Algorithm (0) | 2024.07.15 |
|---|---|
| [AI 5주차] Deep learning의 실용적인 측면 (0) | 2024.07.02 |
| [AI 4주차] DNN(깊은 신경망) (0) | 2024.06.27 |
| [AI 2주차] 신경망 기초 (0) | 2024.06.25 |
| [AI 1주차] Deep Learning 소개 (0) | 2024.06.25 |



