사진이 input으로 주어지면, 우선 edge를 먼저 탐지한다고 했었다.
그렇다면, 어떻게 edge를 탐지할 수 있을까?
Edge Detection

우선 사진이 주어지면, vertical edge detector 를 통해 vertical edges 를 탐지한다. 그리고, horizontal edges detector 를 통해 horizontal edges 를 탐지한다.
그렇다면, 어떻게 vertical edge 를 detect 할 수 있을까?
아래와 같이 6x6 의 grey scale image 가 있다고 해보자. (참고로, rgb channel 일 때는 6x6x3 이다.)
3x3 filter (kernel) 와의 convolution 를 통해 vertical edge를 detect할 수 있다. 4x4 가 된다. (element-wise)

이번에는, 조금 더 단순한 이미지를 가지고 convolution 연산한 결과를 살펴보자.
이미지의 각 element의 숫자가 높을수록 밝고, 낮을수록 어둡다고 할 때, 각 image, filter, output은 아래와 같이 연산된다.

input 이미지를 봤을 때, 중앙에 edge가 있으며 우리는 이것을 detect 하면 되는데, 3x3 vertical edge detection filter를 사용해서 연산을 하게 되면 오른쪽 4x4 output을 얻을 수 있다. 중앙에 아주 밟은 하얀색 부분이 존재하게 되는데, 이 부분에 의해서 vertical edge를 감지할 수 있다.
우리가 input 이미지를 꽤 작은 것으로 사용했기 때문에, 흰색 부분이 꽤 두꺼워 보일 수 있는데, 만약 1000x1000과 같은 고해상도의 이미지를 사용한다면, 이미지의 vertical edge가 더 잘 감지될 것이다.
이번에는 positive edge와 negative edge의 차이점과 다른 유형의 edge detector를 살펴보도록 하자.
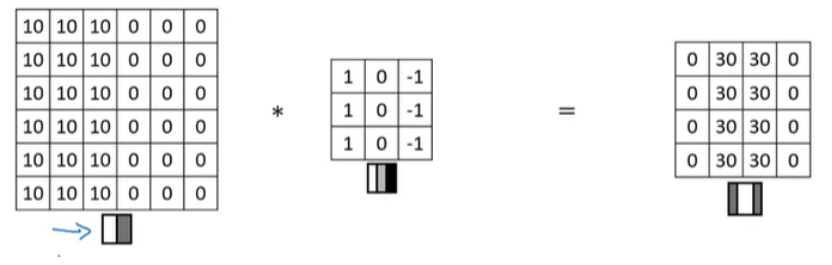
방금 전 위에서 봤던 예시인데, input 이미지가 왼쪽은 밝고 오른쪽은 어두운 이미지이다. 이러한 Edge를 positive edge라고 한다. 그리고 3x3 filter를 conv 연산을 통해서 이미지 가운데에 vertical edge를 감지하도록 했다.
만약 input 이미지의 색상이 뒤집어져서, 왼쪽이 어둡고 오른쪽이 밝게 된다면 어떻게 될까? 이 negative edge인 이미지를 의미한다.

전환되는 명암이 반대가 되기 때문에, 위와 같이 conv 연산 결과값이 -30으로 나타나게 된다. 이것은 edge가 어두운 색에서 밝은 색으로 변환한 것을 감지했다는 의미이고, 만약 positive나 negative를 신경쓰지 않는다면, output matrix에 절대값을 얻어서 사용하면 된다.
horizontal edge detection은 아래의 filter를 사용해서 감지할 수 있다.
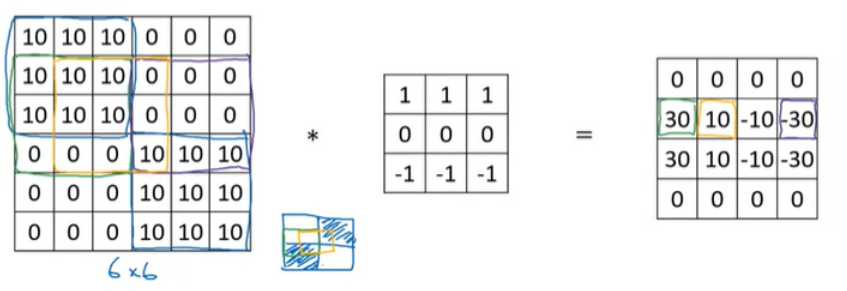
위와 같은 6x6 이미지가 조금 복잡한 예시이긴 하지만, 이 input 이미지를 horizontal edge filter와 convolution 연산을 하게 되면, 오른쪽 4x4 output matrix를 얻을 수 있다. 초록색 박스의 경우에는 10 -> 0으로 변화하는 positive edge의 결과이며, 보라색 박스의 경우는 0 -> 10으로 변화하는 negative edge의 결과이다. 여기서 노란색 박스의 10을 살펴보면, 왼쪽은 positive edge를 감지하고 있고, 오른쪽은 negative edge를 감지하고 있는 것을 볼 수 있다. 따라서 두 edge 감지가 섞여서 중간값을 나타내고 있는것이다. 6x6 이미지는 매우 작기 때문에 체감이 되지 않겠지만, 1000x1000 정도의 이미지라고 한다면, 10이나 -10과 같은 전환영역은 보이지 않게 된다.
다른 예시의 filter 들을 살펴보자.

이렇게 우리가 9개의 숫자를 선택할 수 있는데, 딥러닝에서는 직접 선택할 필요가 없으며, 학습을 통해서 이 값들을 얻게 된다. 즉, 3x3 filter의 경우에는 9개의 학습할 parameter를 갖게 되는 것이다.

그렇기 때문에, 어느 방향의 edge detection이든지 데이터로부터 학습할 수 있다. (이것은 low-level의 feature가 된다)
따라서, CNN에서의 장점은 어떤 특정한 filter를 선택하는 것이 아니라, 학습을 통해서 최적의 filter(일종의 weight)를 얻게 되는 것이다.
Padding
우리는 6x6 이미지에 3x3 filter로 conv연산을 했을 때, output matrix가 4x4의 크기를 갖는 것을 보았다. 4x4 matrix가 되는 이유는 3x3 filter가 input 이미지에 놓일 수 있는 공간이 4x4이기 때문이다. 따라서, (n x n) image * (f x f) filter를 연산하면 (n - f + 1) x (n - f + 1)의 output을 얻을 수 있다.
이 부분에서 2가지 단점이 존재한다.
- convolution 연산을 수행할 때마다 image 가 작아진다. 계속해서 작아진다면, 몇 번의 convolution 연산 밖에 할 수 없게 된다.
- corner 나 edge 에 존재하는 pixel 은 많이 사용하지 않는다. 결국, 버리는 것과 같다.
이렇게 이미지가 conv연산을 할 때마다 줄어든다면, 만약 100개의 deep layer를 가진 network가 있을 때 100 layer 이후에는 너무나 작은 이미지만 남게 되고, 또한 가장자리의 정보들을 버리게 된다.
이 문제점을 해결하기 위해서 우리는 경계에 padding을 추가한다.

위와 같이, 원래 6x6 이미지에 padding을 추가해서 8x8 이미지로 만들고 3x3 filter를 통해서 convolution 연산을 수행하면, output matrix는 입력 이미지와 동일한 6x6 크기의 matrix를 얻을 수 있게 되며, 원본 이미지의 크기를 보존하게 된다.
padding의 정도를 p라고 한다면, (기본 p = 0; no padding) 아래와 같은 공식으로 크기가 결정된다.
(n + 2p, n + 2p) image * (f, f) filter = (n + 2p - f + 1, n + 2p - f + 1) output
padding의 존재에 따라서 두 가지 옵션의 convolution이 있다.
- Valid Convolution : 기본적으로 padding 없이 convolution 연산하는 것을 의미한다.
- Same Convolution : padding을 추가해서 input size가 output size와 동일하도록 convolution연산하는 것을 의미한다.

Same Convolution에 대해서 조금 더 살펴보면, input image가 (n, n), filter가 (f, f), 그리고 padding을 p만큼 적용한다면, output matrix는 (n+2p-f+1, n+2p-f+1)이 된다. 우리는 이 size가 input과 동일하도록 만들기 위해서 방정식으로 정리하면, p=(f−1)/2 로 나타낼 수 있다.
전형적으로 f는 거의 홀수이며, 만약 짝수라면, 비대칭 padding을 해야한다.(f를 홀수로 지정해서 중앙 포지션을 갖도록 하는 것이 computer vision에서 좋은 편이다) f가 홀수인 것이 항상 좋다는 이유는 될 수 없지만, 많은 논문에서 3x3 filter가 흔하며, 5x5, 7x7, 1x1의 filter도 존재하며, 만약 f가 짝수더라도 좋은 성능을 낼 수도 있다.
Strided Convolution
앞서 봤던 계산 방식은 stride 가 1인 상황이라고 생각하면 된다. 즉, 한 칸씩 밀면서 convolution 연산을 거치게 된다.
stride = 2로 설정한다고 하면 다음과 같은 연산된다.
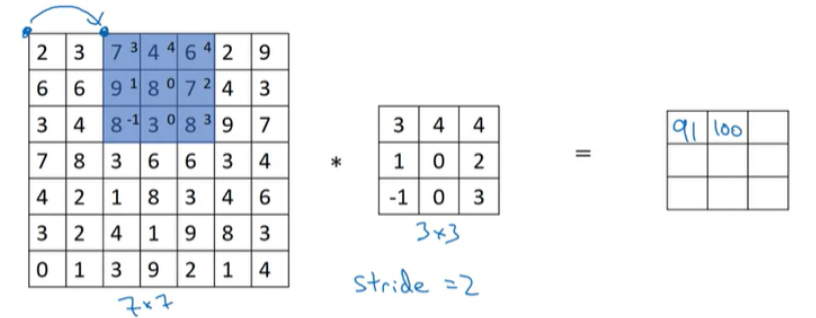
첫 번째 element는 이전과 동일하게 진행하지만, 2번째 element는 원본 이미지에서 2칸 이동해서 element-wise 곱을 수행하게 된다.
그 결과, 우리는 7x7 image와 3x3 filter를 convolution 연산을 통해서 3x3 output matrix를 얻게 된다. input과 output 크기는 다음 공식에 따라서 결정된다. (padding= p, stride= s)

를 의미하며, 만약 정수가 아니라면 소수점은 버리게 된다. 즉, 위에서 파란색 박스가 이미지 내에 완전히 포함될 경우에만 유효하다는 것을 의미한다.
여기서는 p = 0이고, s = 2 이기 때문에, 공식을 적용하면 아래와 같다.

추가로, 수학적인 의미의 convolution과 CNN에서의 convolution은 조금 다르다. 수학적인 의미에서 convolution은 요소간의 곱을 진행하기 전에 수행해야되는 단계가 하나 더 있으며, 이 단계는 filter를 상하좌우 반전을 시켜주는 것이다. 따라서 CNN에서 수행하는 convolution 연산은 실제적으로는 cross_correlation에 해당하지만, 딥러닝에서는 그냥 convolution이라고 부른다.
Convolutions Over Volume
지금까지 2D에서의 convolution 연산을 살펴보았고, 이제는 3D volume에서 어떻게 conv연산을 수행하는지 살펴보자.
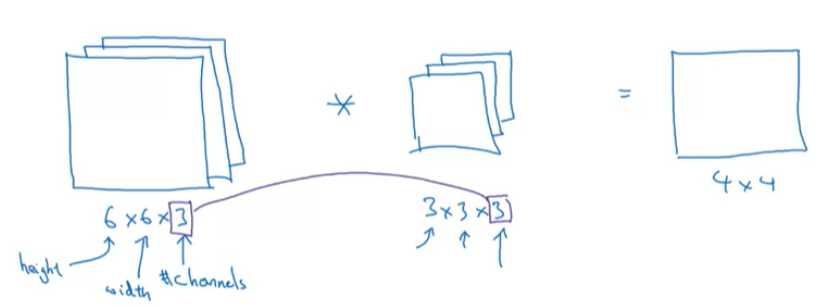
우선 RGB channel을 가지고 있는 이미지를 convolution 연산을 수행한다면, 연산에 사용되는 filter의 channel은 input 이미지의 channel과 동일해야 한다. 이렇게 연산을 하게 되면, ouput은 4x4가 되는데, 이것은 4x4x"1" 이 된다. 어떻게 연산되는지 자세하게 살펴보자.
일반적인 conv연산과 거의 동일하며, 차이점은 input과 filter를 각각의 채널에서 요소간의 곱을 수행한다. 그러면 각 채널마다 9개의 결과값이 나오고, 총 27개의 결과값이 나오게 된다. 그리고 이 결과값들을 모두 더해주면, 최종 output이 되는 것이다. 나머지 element들도 기존과 동일한 방법으로 구하고, 채널끼리 conv 연산을 수행해서 모두 더해주면 된다.

그리고, 만약 R Channel에서만 Edge를 감지하고 싶다면, R channel만 채워고, 나머지 channel은 전부 0으로 채우면 된다.

또는, vertical edge의 색상을 신경쓰지 않는다면, 3가지 channel에 모두 동일하게 vertical edge detector로 만들 수 있으며, 이렇게 만든다면 어느 색상의 모서리도 감지할 수 있는 filter가 된다.

위의 예시는 하나의 필터를 사용해서 결과는 2-dim으로 나타나는 것을 보여주고 있다.
만약 우리가 동시에 여러 filter를 사용하고 싶다면 어떻게 해야 할까?

만약 동시에 2가지 filter를 사용하기 원한다면, 위와 같이 각각의 filter(여기서는 vertical edge와 horizontal edge detector)에 대해서 conv연산을 수행하고, 결과 matrix를 쌓으면 된다. 따라서, 결과는 4x4x2의 matrix가 된다.
요약하자면, 다음과 같이 나타낼 수 있다.

여기서 n_c는 input 이미지의 channel을 의미하고, n_c′는 filter의 수를 의미한다.
이렇게 filter의 수를 추가함으로써 다른 feature들을 동시에 감지할 수 있도록 해준다.
여기서 input의 마지막 dimension을 channel의 수라고 언급했는데, volume의 'depth'라고 부르기도 한다.
One Layer of a Convolution Network
이제 CNN에서 하나의 layer를 어떻게 구성하는지 살펴보도록 하자.

이전 강의까지 우리는 input 이미지를 filter를 통해 conv연산을 수행했는데, 연산을 수행하고 bias를 추가한 후에 non-linear(ReLU)를 적용한다. 이 과정이 하나의 CNN layer가 된다.
우리가 잘 아는 공식으로 나타낸다면, 다음과 같이 나타낼 수 있을 것이다.

filter들이 w^[1] 와 같은 역할을 하게 된다.
이 예제에서는 2개의 filter를 사용했기 때문에, output이 4x4x2로 나타나고, 만약 10개의 filter를 사용했다면, 4x4x10의 결과를 얻을 수 있다.
만약 CNN Layer에서 3x3x3의 filter 10개를 사용한다면, 이 layer에서 파라미터의 개수는 어떻게 될까?

하나의 filter를 먼저 살펴보면, 각 filter는 3x3x3=27 parameters와 1개의 bias가 존재하며, 따라서 하나의 filter에는 28개의 parameter가 존재한다. 따라서, 총 280개의 파라미터가 존재하게 된다.
여기서 CNN의 장점이 나타나는데, input 이미지의 크기가 아무리 크다고 하더라도 파라미터의 수는 280개로 항상 고정되어 있다. 따라서, 매우 큰 이미지가 있더라도 overfitting하지 않도록 할 수 있게 된다.
지금까지 사용한 notation을 정리해보면 다음과 같다.

이제 input/output, filter의 크기에 관한 notation을 살펴보자.
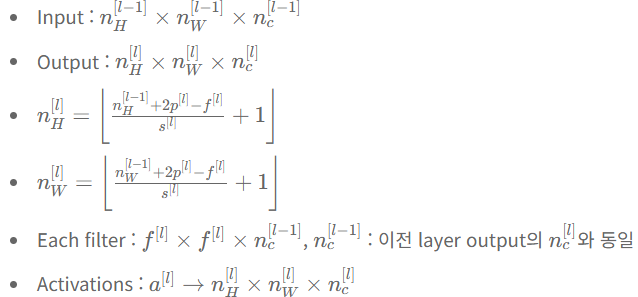
Example of Simple CNN
아래는 ConvNet의 예시이다.

convolutional network 에는 3가지 layer가 있다.
- Convolution (Conv Layer)
- Pooling (POOL Layer)
- Fully connected (FC Layer)
Pooling Layer
: Conv Layer 이외에도 CNN은 pooling layers 를 사용하여 표현 크기를 줄임으로써 계산 속도를 높이고 특성을 훨씬 더 잘 검출해낼 수 있다.
-Max Pooling

4x4 input 이 있을 때, 이를 4개의 다른 region 으로 나누고 각각에 대한 max 값을 사용한다. 결국, 2x2 output 이 된다.
여기서 hyperparameter 에 대해서 생각해보면, f = 2 이고, s = 2 이다.
이유는 모르지만, 성능이 좋다.
-Average Pooling

이전과 유사한 계산 방식인데, average를 취한다는 것이 차이점이다.
hyperparameter를 정리해보면 다음과 같다.
- f : filter 의 size
- s : stride
- Max or average pooling
가장 일반적인 값은 2x2 (f=2) 이다. 패딩은 거의 사용하지 않는다.(p=0) 계산을 했을 때, 입력의 채널과 출력의 채널은 일치하는데 풀링은 각 채널에 개별적으로 적용되기 때문이다.한 가지 유의할 점은 Pooling 에서는 학습할 변수가 없다는 것이다. 이는 CNN의 one layer 에서 계산하는 고정 함수이고 학습할 것이 없다.

'연구실 > 인공지능(Coursera)' 카테고리의 다른 글
| [AI 10주차] Object Detection (1) | 2024.08.09 |
|---|---|
| [AI 9주차] 심층 컨볼루션 모델(Deep convolution model) (0) | 2024.08.07 |
| [AI 7주차] Hyperparameter Tuning, Batch Normarlization, and Programming Frameworks (0) | 2024.07.26 |
| [AI 6주차] Optimization Algorithm (0) | 2024.07.15 |
| [AI 5주차] Deep learning의 실용적인 측면 (0) | 2024.07.02 |



