여러 연구/논문에서 CNN의 효과적인 Building Block 구성 방법이 연구되었으며, 이런 예시들을 참고하는 것이 CNN으로 학습할 때 유용하다.
현대 Computer Vision의 토대가 되는 Classic Networks는 아래와 같은 것들이 있다.
- LeNet-5
- AlexNet
- VGG
그리고, 이번에는 CNN에서 유용하게 사용되는 ResNet or Convolution Residual Network와 Inception Neural Network를 알아볼 것이다.
Classic Networks
LeNet-5

[Input -> Conv2D -> Avg Pool -> Conv2D -> Avg Pool -> FC -> FC -> output]
LeNet-5의 구조는 위와 같다.
위 논문이 작성될 시기에는 Average Pooling이 많이 사용되었으며, padding이나 valid convolution을 사용하지 않았다. 그리고 논문에는 non-linearity(비선형)로 ReLU가 아닌 sigmoid나 tanh 함수를 많이 사용했다.(당시에 비선형성을 사용하지 않았음)
LeNet의 구조는 신경망이 깊어질수록 높이와 폭 (N_H,N_W) 이 줄어드는 경향이 있고, 채널 수(N_C)는 증가하고 있다. output에는 최근에는 softmax를 많이 쓰지만, 당시에는 다른 분류기를 사용했고, 현재보다 작은 신경망으로 약 60,000개의 파라미터를 가지고 있다.
AlexNet

AlexNet의 구조는 위와 같고, LeNet과 유사한 구조를 가지고 있지만, 더 크다는게 차이점이다. 약 6천만개의 파라미터가 존재한다. 여기서는 비선형으로 ReLU를 사용하며, Multiple GPU도 사용한다. 그리고 Local Response Normalization(LRN)을 사용했는데, 연구를 통해서 성능에 크게 영향을 미치지 않는다고 밝혀졌고 최근에는 잘 사용하지 않는다.
VGG-16

여기서 주목할 만한 점은 많은 하이퍼파라미터를 가지고 있지만, 네트워크를 더 단순하게 만들었다는 것이다. [ConV(3x3 filter, strides=1, same convolution) -> Max Pool(2x2 filter, strides=2)] 로 구성된 network를 반복해서 사용한다.
VGG-16 이름에서 유추할 수 있듯이 16개의 layer로 구성되어 있으며, 약 1억 3800만개의 파라미터가 있다. 이 수치는 오늘날에도 매우 큰 값이고, 학습시킬 파라미터가 매우 많은 큰 네트워크이다. 하지만, 네트워크가 매우 단순하고 균일한 구조를 가지고 있다는 점에서 매력적이다. VGG-19가 조금 더 큰 네트워크이지만, VGG-16과 거의 유사하다.
ResNets
아주 Deep한 신경망은 Vanishing Gradient, Exploding Gradient와 같은 문제가 발생하기 때문에 학습시키기가 어렵다.
이 문제를 해결하기 위해서 하나의 layer에서 activation을 취해서 더 깊이 있는 layer에 제공하는 skip connection에 대해서 알아볼 것이다. 이 방법을 사용하면 아주 Deep한 네트워크를 학습시킬 수 있는 ResNet을 만들 수 있다. 심지어 100개가 넘는 layer로 구성된 네트워크도 학습이 가능하다.
ResNet은 Residual Block이라는 것으로 구성되어 있다. Residual Block은 다음과 같다.

위와 같이 a^[l]이 2개의 layer를 초록색의 main path로 지나게 되면 a^[l+2]를 얻을 수 있다. Residual Block에서는 입력인 a^[l] 을 바로 다음 layer를 뛰어넘고, 그 다음 layer(ReLU를 적용하시키기 전)로 연결시켜준다. 이 path를 shortcut이라고 부르며, a^[l] 의 정보가 shortcut을 따라 더 깊은 layer로 바로 전달된다.
따라서 마지막 값은 아래와 같다.

정리하자면, a^[l] 이 layer 를 하나 혹은 두개씩 건너뛰는 것을 의미한다. ResNet의 구성하는 방법은 이런 Residual Block들을 많이 사용해서 DNN을 구성한다.
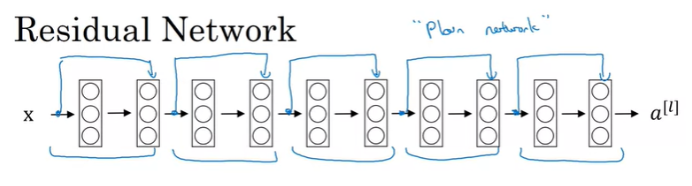
논문에 사용되는 용어로 shortcut이 없는 일반적인 NN을 Plain Network라고 한다.

반면에, ResNets은 아래와 같이 Residual Block으로 이루어진 네트워크이며, 만약 Residual Block, Shortcut없이 학습을 수행한다면, 아래 왼쪽 그래프처럼 네트워크가 더 깊어질수록 성능이 안 좋아지는 것을 볼 수 있다. 하지만, ResNet을 사용한다면 Deep Network를 학습하는데 효과적이다.

위 결과는 layer가 많아져도 train error를 저하시킬 수 있다는 것을 보여주고 있고, ResNet을 사용하면 중간에 있는 activation이 더 깊이 전달되어서 vanishing/exploding gradient 문제를 해결되는 것이다.
그렇다면 왜 ResNet이 Deep Network에서 잘 동작하는 것일까?

위와 같은 구조가 있고, network 전체에 걸쳐서 activation function으로 ReLU를 사용한다고 가정한다면, 모든 activation은 0보다 크거나 같을 것이다.(Input은 예외가 있을 수 있음)
그리고 skip connection의 shortcut에 의해서 다음과 같은 식이 성립한다.
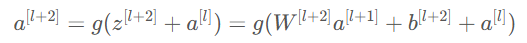
만약 L2 Regularization을 사용한다면 W^[l+2] 가 줄어드는 경향이 있을 것이고, bias에도 적용하고 있다면, b^[l+2] 도 줄어들 수도 있다.
극단적으로 W^[l+2]=0, b^[l+2]=0이라고 가정해보자.
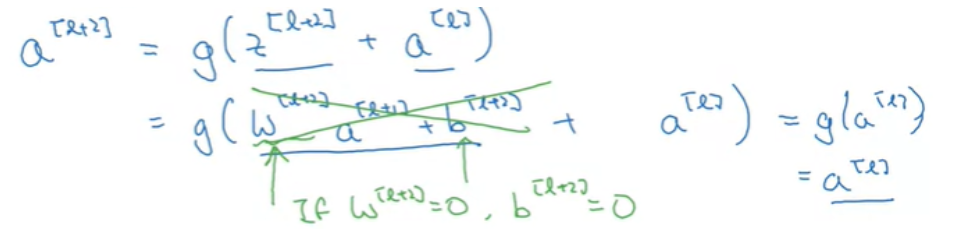
그렇다면 결국 a^[l] 만 남게 된다. (ReLU이기 때문에) 따라서, a^[l+2]=a^[l] 이라는 것을 보여주고 있고, 또한, Identity function을 학습하는 것은 쉽기 때문에 신경망의 성능을 저하시키지 않는다는 것을 보여준다. 만약, residual block이 없는 deep network에서는 Identity function을 위한 파라미터 선택(학습)이 어렵고, 성능이 떨어진다.
한 가지 주의해야하는 것은 z[l+2]와 a[l]이 같은 dimension을 가져야한다는 것이다. 그래야 shortcut을 적용할 수 있다. 만약 다른 dimension을 갖는다면, 추가 matrix를 사용해서 차원을 동일하게 만들어 줄 수도 있다.
a^[l+2]=g(z^[l+2]+W_s * a^[l])
여기서 W_s는 파라미터일 수도 있고, 고정된 matrix일 수도 있다.
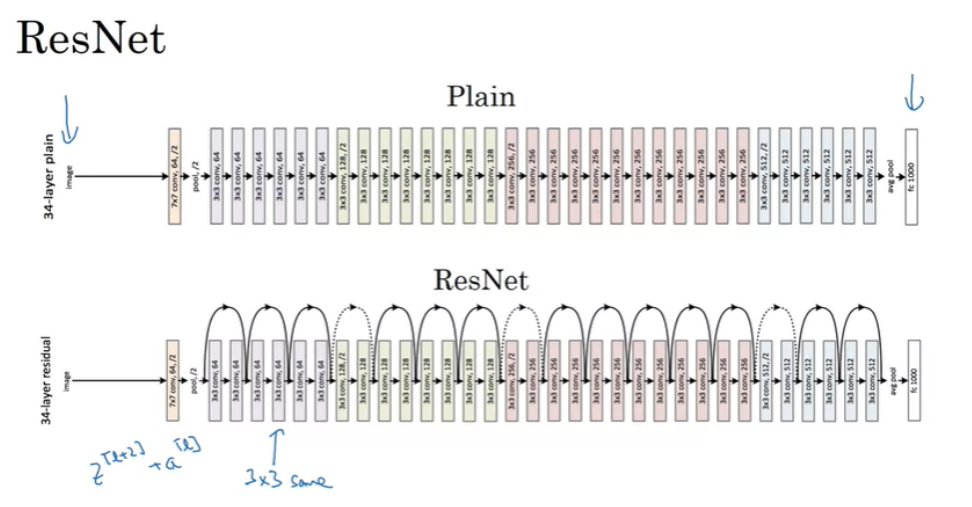
위 이미지는 논문에 있는 이미지이다. 그리고 'same convolution'을 사용하기 때문에 z^[l+2],a^[l] 의 dimension은 일치하게 된다. 만약 다른 Conv나 pooling이 추가되면 W_s 와 같은 것으로 dimension을 조정해주어야 한다.
Network in Network and 1x1 Convolutions
CNN 설계에 있어서 1x1 convolution을 사용하는 것은 아래와 같은 장점을 가지고 있다.
- Channel 수 조절
- 연산량 감소
- 비선형성
만약 28x28x192 volume이 있을 때, 높이와 넓이를 줄이고 싶다면 Pooling layer를 사용하면 된다.
채널이 너무 많아서, 채널을 줄이고 싶다면(28x28x32로), 32개의 1x1 filter를 사용하면 된다. 각각의 filter는 1x1x192이다.
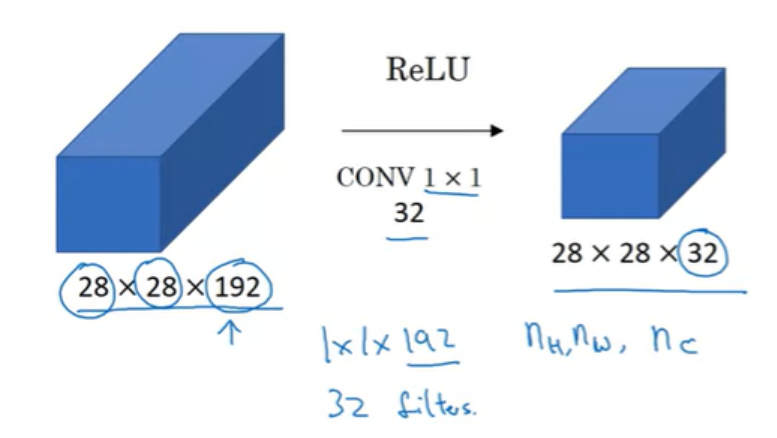
만약 채널의 수를 192로 유지하고자 한다면, 아래와 같이 filter수를 설정하면 된다.

Inception Network Motivation
아래는 Inception Module이며, feature들을 효과적으로 추출하기 위해서 Conv(1x1, 3x3, 5x5)와 Max-Pooling(3x3)을 각각 수행해서 output을 쌓아올린다. 아래에서는 28x28x192 volume은 Inception Modeul을 통해서 28x28x256 volume이 된다.

기본 아이디어는 네트워크가 원하는 파라미터가 무엇이든, 원하는 filter 사이즈 조합이 무엇이든, 이것들을 모두 다 학습하게 하는 것이다. 하지만, 한 가지 문제점이 존재하는데 연산량이 너무나 많다는 것이다. 5x5 Conv에 대해서 연산량이 얼마나 되는지 한 번 알아보자.

28x28x192 volume에 대해서 5x5 'same' conv 연산을 수행하면, 28x28x32x5x5x192로 1억2천만번의 연산이 수행된다.
여기서 방금 전에 언급했던 1x1 Convolution을 적용하면 어떻게 될까?
연산량을 약 10배정도 감소시킬 수 있다.
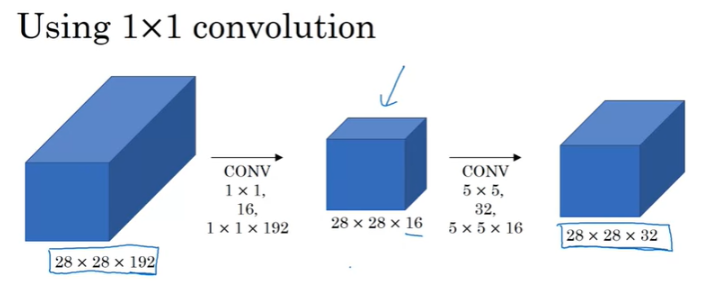
방금 전의 5x5 Conv연산에서 중간에 1x1 Conv 연산을 추가했는데, bottleneck layer(병목층)이라고 부르기도 한다. 중간 과정을 통해서 16채널로 감소시키고, 5x5 Conv 연산을 진행하게 된다. 연산량은 28x28x16x1x1x192(1x1 conv 연산) + 28x28x32x5x5x16(5x5 conv 연산)으로 2.4M + 12.4M이며, 약 1240만으로 1억2천만에서 약 10배정도 감소되었다.
요약하자면, 만약 신경망을 구성할 때, 어떤 layer를 사용할지 잘 모르겠다면 inception module을 사용하면 된다. 하지만 연산량 문제가 있기 때문에 1x1 Conv를 추가해서 연산량을 크게 줄일 수 있었다. 다만, 1x1 Conv를 추가하는 것이 신경망의 성능을 떨어지게 하는 것이 아닌지 의심할 수도 있다. 이 bottlenect layer를 구현함으로써 channel 수를 감소시키며, 성능을 떨어뜨리지는 않는 것처럼 보이고, 연산량을 줄일 수 있다.
이것이 inception module의 기본 아이디어이고, 계속해서 어떻게 full inception network를 구성할 수 있는지 알아보자.
Inception Network
방금까지 기본직인 Inception Building Block을 살펴보았고, 이 block을 결합해서 Inception Network를 구현해보도록 하자.
Inception Module은 아래과 같이 구성되며, input은 이전 layer에서 나온 activation을 사용한다. 방금 보았던 28x28x192를 input으로 사용해보자.
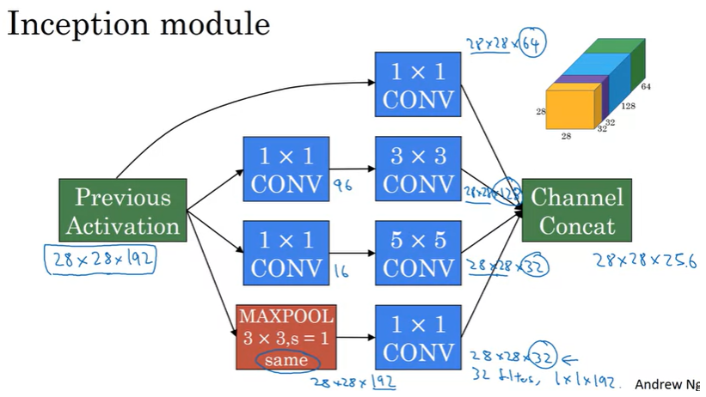
위와 같이 input 28x28x192를 1x1 Conv / 1x1 Conv->3x3 Conv / 1x1 Conv->5x5 Conv / MAXPOOL->1x1 Conv 을 각각 거치도록해서 나온 결과를 합쳐서 28x28x256의 output을 얻는다. MAXPOOL layer 뒤에 1x1 Conv layer가 오는 것에 유의한다(MAXPOOL을 통해서는 channel 수를 감소시킬 수 없어서, 1x1 Conv를 사용해서 channel 수를 줄여준다).
이런 block들을 합쳐서 아래와 같은 모델을 구성할 수 있다.

모델을 보면 알겠지만, 모델 초반에는 Inception Module이 들어가지 않는다.(Stem 영역이라고 하는데, 일반적인 Conv-Pool 스타일을 가지고 있고, 초반에는 Inception 효과가 크지 않다고 한다.)

논문에서는 초록색으로 표시된, 모델 output layer 말고, 보조로 사용되는 softmax layer 가 존재한다. 이는 파라미터가 잘 업데이트되도록 도와주며, output 의 성능이 나쁘지 않게 도와준다. 또한, regularization 효과를 얻을 수 있고, overfitting 을 방지한다.
위 모델은 Google의 개발자들에 의해서 만들어졌고, GoogLenet이라고 부른다. 이 모듈을 기반으로 다른 버전을 만든 것도 있으며, Inception v2, v3, v4와 residual block과 결합된 inception network도 있다.
MobileNet
지금까지 설명한 신경망들은 상당히 비용이 많이 든다는 것을 알 수 있다. 배포 시에 사양이 낮은 CPU, GPU 를 가진 device 로 neural network 를 실행하고자 하기 위해서 도입된 개념이다. 여기서는 depthwise separable convolution 을 사용한다. normal convolution 과 비교해보자.

우선, 아래는 Normal Convolution 연산 방식이다.

Depthwise separable convolution 은 Depthwise Convolution 이후에 Pointwise Convolution 을 거친다.
- Depthwise Convolution

input image가 6 x 6 x 3 이고, filter 의 size가 3 x 3 이라고 하자. (filter 는 2D이다.)
여기서, 주의할 점은 filter의 개수가 input 의 channel 과 같다는 것이다. 이렇게 계산하면 4 x 4 x 3 이 output size가 된다. 하지만, 4 x 4 x 5 가 되기 위해서는 추가적인 계산 과정이 필요하다. pointwise convolution을 거친다.
2. Pointwise Convolution

pointwise convolution은 normal convolution 방식과 비슷하다. filter의 개수만큼 channel이 output으로 생긴다.
이제, Normal Convolution 방식과 Depthwise seperable Convolution 의 Cost 를 비교 정리해보자.
- Normal Convolution : 2160
- Depthwise seperable Convolution : 432 + 240 = 672
이 경우에는 672 / 2160 = 약 0.31 이므로 Depthwise seperable Convolution이 Normal Convolution 에 비해서 31 % 비싸다고 할 수 있다. MobileNet 논문 저자는 일반적으로 1 / n_c' + 1 / (f^2) 만큼 비싸다고 한다. 여기서 n_c' 은 filter 의 개수이고, f 는 filter 의 size 이다.
MobileNet Architecture
앞서 언급한 MobileNet에는 version이 1과 2가 있다. 여기서 projection 은 pointwise convolution 이다.

v1 는 depthwise separable convolution 이 13번 반복된다. v2 는 v1에서 residual connection(skip connection) 이 적용된 것이지만, depthwise 이전에 expansion 과정이 추가되고 17번이 반복된다. 빨간색 부분을 더 자세하게 살펴보자.
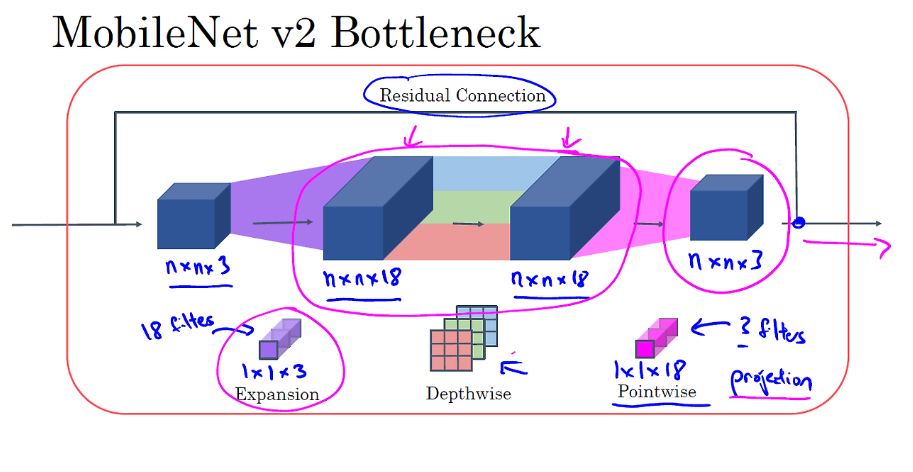
그렇다면, bottleneck 이 왜 필요할까?
expansion 과정을 통해 neural network 가 더 풍부한 function 을 학습할 수 있도록 해줄 수 있고, mobile device 의 배포 과정에서 memory 제약이 있기 때문에 pointwise 과정을 통해 줄여줄 필요가 있기 때문이다.
Efficient Net
이제 MobileNet V1과 V2를 통해 계산 효율이 높은 신경망을 구현하는 방법을 알게 되었다. 그런데 특정 장치에 맞게 MobileNet이나 다른 아키텍처를 조정할 방법이 있을까?
만약 계산 자원이 조금 더 있다면, 조금 더 큰 신경망을 사용하여 정확도를 조금 더 높일 수 있기를 바랄 것이고, 반대로 계산 자원이 제한적이라면, 조금 더 작은 신경망을 사용하여 실행 속도를 조금 더 빠르게 하되, 약간의 정확도를 희생할 수도 있을 것이다. 그러면 특정 장치에 맞게 신경망을 자동으로 확장하거나 축소할 방법이 있을까? EfficientNet이 바로 그렇게 할 수 있는 방법을 제공한다.
입력 이미지의 해상도(r)와 신경망의 깊이(d), 레이어의 너비(w)를 어떻게 설정할지를 고민할 수 있다. EfficientNet 논문의 저자는 이러한 세 가지 요소를 조정하여 신경망을 확장하거나 축소할 수 있다고 관찰했다. 해상도가 높은 이미지를 사용할 수도 있고, 신경망의 깊이를 깊게 할 수도 있으며, 레이어를 더 넓게 만들 수도 있다. 이 세 가지 요소를 동시에 조정하는 복합 스케일링(compound scaling)을 통해 이미지 해상도, 신경망의 깊이, 레이어의 너비를 동시에 확장하거나 축소할 수 있다.

여기서 중요한 점은, r, d, w를 확장하거나 축소할 때 각 요소를 어떤 비율로 조정해야 하느냐는 것이다. 해상도를 두 배로 늘리고 깊이나 너비는 그대로 두어야 할까? 아니면 깊이를 두 배로 늘리되 다른 요소는 그대로 둘까? 또는 해상도를 10% 늘리고, 깊이를 50% 늘리며, 너비를 20% 늘리는 것이 좋을까? 주어진 계산 자원 내에서 최적의 성능을 얻기 위해 r, d, w 사이의 균형을 어떻게 맞추어야 할까? 특정 장치에 맞게 신경망 아키텍처를 조정하려고 할 때, EfficientNet의 오픈 소스 구현 중 하나를 참고하여 r, d, w 간의 균형을 잘 맞추는 방법을 찾아볼 수 있다.
'연구실 > 인공지능(Coursera)' 카테고리의 다른 글
| [AI 11주차] Face Recognition (얼굴 인식) & Neural Style Transfer(신경 스타일 전송) (1) | 2024.08.10 |
|---|---|
| [AI 10주차] Object Detection (1) | 2024.08.09 |
| [AI 8주차] Convolution Neural Network (CNN) 기초 (0) | 2024.08.05 |
| [AI 7주차] Hyperparameter Tuning, Batch Normarlization, and Programming Frameworks (0) | 2024.07.26 |
| [AI 6주차] Optimization Algorithm (0) | 2024.07.15 |



