Fuzzing(퍼징)
: software의 취약점을 test하는 기법 중 하나이다. 위의 예시와 마찬가지로, software에 input값을 무작위로 대입해보고, 그 process에서 발생하는 error나 collision을 monitoring해서 security의 허점을 찾아내는 방식이다.
fuzzing에 대해서 공부를 하기 전에 software testing의 개념이 알아야 한다.
Software testing
: software를 어떻게 test 하고, 이 test가 성공적인지 아닌지, 충분하게 testing 되었는지를 어떻게 판단할 수 있을까?
아래 square root function 예제 코드를 보자.
def my_sqrt(x):
"""Computes the square root of x, using the Newton-Raphson method"""
approx = None
guess = x / 2
while approx != guess :
approx = guess
guess = (approx + x / approx ) / 2
return approx
이 function이 실제로 잘 작동하는지를 알아내야 한다. 위의 코드는 python으로 작성되었다.
우선, python programs를 이해해야 한다.
- python은 들여쓰기를 통해 programs을 구성한다. 그래서, function과 while문은 들여쓰기를 통해 정의된다.
- python은 동적타입 언어이다. 즉, approx, guess, x 변수는 run-time에 결정된다.
- python 대부분의 문장은 제어문(while, if), 비교문(==, !=, <)와 같은 다른 공통 언어에 의해 영감을 받았다.
이러한 개념을 가지고, 위의 code를 이해할 수 있다.
guess = x / 2 로 시작해서, approx 값이 더이상 변하지 않을 때까지 계산하고 approx 값이 return된다.
Running a Function
이제, 위의 코드를 실행해보자. (colab에서 실행)

올바른 값을 잘 산출하는 것을 확인할 수 있다.
다른 입력값으로 기능을 다시 확인해보자.

마찬가지로, 기능이 잘 동작하는 것을 확인할 수 있다.
Debugging a Function
이제, function을 debugging 해보자.
my_sqrt() 이 어떻게 작동하는지 알기 위해서, 중요한 지점에 print()를 찍어보는 것은 좋은 전략이다.
def my_sqrt_with_log(x):
"""Computes the square root of x, using the Newton-Raphson method"""
approx = None
guess = x/2
while approx!=guess:
print("approx=", approx) # <--New
approx = guess
guess = (approx + x/approx) / 2
return approx
위의 코드를 실행해보자.
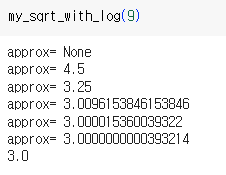
Checking a Function
다시, testing으로 돌아가서 코드를 보자. my_sqrt(2) 값이 실제로 올바른 값인지 확실하지 않을 수 있다.
그래서, sqrt(x) * sqrt(x) = x 라는 식을 이용해서 입증해보자

my_sqrt () 가 올바른 함수라면 2라는 값이 나와야 한다. 하지만, 위의 결과를 통해 오류가 있음을 알 수 있다.
Automating Test Execution
이처럼, 직접 손으로 program을 testing 할 수 있지만, 매우 제한된 양의 실행과 결과만 확인할 수 있고 program이 바뀌면 testing process를 다시 반복해야하므로 다소 비효율적이다. 그래서, testing 을 자동화하는 것은 유용하다. computer가 계산을 하도록 하고 결과를 체크하는 것이 단순한 방법이다.
sqrt(4)가 2인지 아닌지를 자동으로 testing하는 예시를 살펴보자.
result = my_sqrt(4)
expected_result = 2.0
if result == expected_result:
print("Test passed")
else:
print("Test failed")
이러한 testing의 장점은 계속해서 실행해볼 수 있다는 것이다. 하지만 몇가지 문제가 있다.
- 단일 test를 위해서 5 line의 code가 필요하다
- rounding error를 고려하지 않는다
- 오직 단일 input(단일 result)만 확인할 수 있다
모든 programming 언어는 조건문이 지켜지는지 아닌지 만약 지켜지지 않는다면 실행을 멈추는지 아닌지를 자동으로 확인하는 assertion 기능을 가지고 있다. 이는 testing에서 매우 중요하다. python에서 assert문은 조건을 취하고, 조건이 성립하면 아무것도 일어나지 않는다. 반면에, 조건문이 거짓이라고 평가한다면, assert는 예외를 일으키고 test가 실패했다고 지시한다.
my_sqrt() 이 expected result를 산출하는지 아닌지를 쉽게 확인하기 위해 assert를 사용해볼 수 있다.
assert my_sqrt(4) == 2
위의 코드의 결과는 true이기 때문에 아무 일도 일어나지 않는다는 것을 알 수 있다.
floating-point를 계산하는 과정에서 rounding error가 발생할 수 있다. 그래서 우리는 2개의 floating-point 값이 동일한지 아닌지를 비교할 수 없다. 그래서, threshold value를 이용해서 비교를 하게 된다. 전형적으로 epsilon을 사용한다.
EPSILON = 1e-8
assert abs(my_sqrt(4)-2) < EPSILON
위의 코드를 실행해보면 아무 일도 일어나지 않는다. 위의 과정을 함수화하여 편리하게 할 수 있다.
def assertEquals(x,y, epsilon=1e-8):
assert abs(x-y) < epilson
이처럼 program이 올바르게 동작하는지 확실하게 하기 위해 계속해서 asserting을 사용할 수 있다.
Generation Tests
우리는 아래 식이 항상 성립한다는 사실을 알고 있다.
sqrt(x) * sqrt(x) = x
이를 바탕으로 testing을 할 수 있다.
for i in range(1, 1000):
assertEquals(my_sqrt(i) * my_sqrt(i), i)
위의 코드를 실행할 때, 얼마나 시간이 걸리는지 확인하기 위해서 Timer module을 사용할 수 있다.
import bookutils.setup
from Timer import Timer
with Timer() as t:
for n in range(1, 10000):
assertEquals(my_sqrt(n) * my_sqrt(n), n)
print(t.elapsed_time())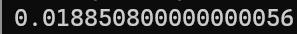
Automatic run-time check
my_sqrt()를 쓰고, test를 하는 것 대신에 check를 바로 구현으로 통합하여 자동으로 run-time check할 수 있다.
def my_sqrt_checked(x):
root = my_sqrt(x)
assertEquals(root*root, x)
return rootprint(my_sqrt_checked(2.0))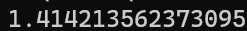
이와 같은 automatic run-time check는 2가지를 가정한다.
- run-time check를 공식화해야 한다.
check하기 위한 구체적인 값을 항상 가져야 한다. 하지만, 바람직한 속성을 추상적인 양식으로 공식화하는 것은 복잡할 수 있다. 실제로, 어떤 속성이 가장 중요한지를 결정할 필요가 있고, 그들을 위한 적절한 check를 설계해야 한다. 따라서, run-time check는 local 속성에 뿐만 아니라 program 상태의 몇몇 속성에 의존할지도 모른다. - run-time check를 할 여유가 있어야 한다.
my_sqrt()의 경우에 check는 비싸지 않다. 하지만, 만약에 대규모 data 구조를 단순한 연산 이후에 check해야 한다면, check의 비용이 상당할 것이다. 실제로 run-time check는 전형적으로 생산 동안에 효율성을 위해 버려진다. 반면에, run-time check의 comprehensive한 suites는 error를 발견하고 그것들을 빠르게 debug하는 좋은 방식이다. 생산하는 동안에 얼마나 많은 이러한 용량을 원하는지를 결정해야 한다.
하지만, 이러한 automatic run-time check에도 한계점이 존재한다. result 가 check 될 때만 correct 를 보장하고, 그렇지 않으면 보장하지 못한다. symbolic한 verification 기술과 program 증명과 반대된다.
System Input vs Function Input
다른 programmer들이 자신의 코드에 이용 가능한 my_sqrt()를 embedding 하도록 할 수 있다. 제 3자로부터 기인한 input을 처리해야 할 것이다. 이는 다른 programmer가 통제하는 것이 아니다.
아래 sqrt_program() 에서 이러한 system input을 simulate해보자.
def sqrt_program(arg: str) -> None:
x = int(arg)
print('The root of', x, 'is', my_sqrt(x))
sqrt_program은 아래와 같이 command line에서 system input을 허용하는 program이다.
$ sqrt_program 4
2
우리는 쉽게 sqrt_program()을 몇몇의 system input으로 호출할 수 있다.
sqrt_program("4")
하지만, 외부 input의 타당성을 check하지 못하는 문제가 있다. sqrt_program(-1)을 호출하면 확인해볼 수 있다.
sqrt_program(-1)
이와 같이 my_sqrt()를 음수로 호출하면 무한 loop에 빠진다. 이를 ExpectTimeout을 이용해서 문제를 해결할 수 있다.
from Timeout import GenericTimeout
with GenericTimeout(1):
sqrt_program("-1")
위의 error message는 TimeoutError가 발생했음을 알 수 있다.
하나의 exception으로 code를 마무리하고 싶지 않으므로 이를 확장해보자. 외부 input을 받아들일 때, 적절하게 타당하게 됐는지를 확실하게 해야한다.
def sqrt_program(arg: str)->None:
x = int(arg)
if x < 0 :
print("Illegal Input")
else :
print("The roof of', x, 'is', my_sqrt(x))sqrt_program("-1")
숫자로 sqrt_program를 호출하지 않을 때는 다음과 같이 exception이 발생한다.
sqrt_program("xyzzy")
이러한 예외도 포함해서 다음과 같이 code를 작성할 수 있다.
def sqrt_program(arg: str)->None:
try:
x = int(arg)
except ValueError:
print("illegal input")
else:
if x<0:
print("illegal number")
else:
print("the roof of", x, "is", my_sqrt(x))sqrt_program("4")
sqrt_program("-1")
sqrt_program("xyzzy")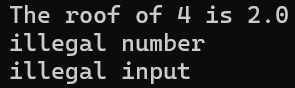
이와 같이 system level에서 program이 통제되지 않은 상태로 들어가지 않고 input을 잘 다룰 수 있다. 물론, programmer에 대한 부담이 있지만, 이러한 부담은 software test를 만들 때 benefit이 될 것이다. 만약 program이 잘 정의된 error message를 가지고 input을 다루면 우리는 어떠한 종류의 input도 보낼 수 있다. 또한, function을 만들어진 value로 호출할 때, 정확한 전제 조건을 알 수 있게 된다.
The Limits of Testing
testing에 있어서 최선의 노력을 들였지만, 항상 유한 집합의 input들에 대해서 기능성을 check해야 한다는 것을 염두에 두어야 한다. 즉, function이 fail할지도 모르는 test되지 않은 input들이 항상 있을지도 모른다.
my_sqrt()의 경우에, √0 를 계산하면 ZeroDivisionError 를 초래할 것이다.
sqrt_program(0)
x 가 0인 경우에도 따로 처리를 할 수 있다.
def sqrt_program(arg: str)->None:
try:
x = int(arg)
except ValueError:
print("illegal input")
else:
if x<0:
print("illegal number")
elif x==0:
print("0")
else:
print("the roof of", x, "is", my_sqrt(x))
광범위한 testing은 우리에게 올바른 program으로의 높은 자신감을 줄지도 모르지만, 모든 미래의 execution이 올바를 것이라는 것을 보장하지는 못한다. 모든 result를 check하는 run-time verification 조차도, result 가 나와야만 result가 올바르다는 것을 보장할 수 있다. 하지만, 미래의 execution들이 failing check 로 이어지 않을지도 모른다는 보장은 없다. fuzzing book의 저자는 my_sqrt_fixed(x) function이 모든 유한 실수 x에 대해서 올바른 √𝑥 의 implementation이라고 믿지만, 아직도 확실하다고 생각하지는 않는다고 한다.
Newton-Raphson method을 통해 implementation이 올바르다는 것을 증명하는 좋은 기회가 될 수 있다. implementation은 단순하고, math는 잘 이해된다. 불행히도 이는 아주 적은 영역에 대한 경우이다. 만약 우리가 본격적인 올바른 증명을 하고 싶다면, testing의 좋은 기회는 다음 2가지이다.
- 몇몇의 잘 선택된 input들로 program을 테스트하기
- 광범위하게 자동적으로 result를 check하기
우리가 완전히 program을 test 할 수 있도록 도와주는 기술과 상태가 올바르다는 것을 check 할 수 있도록 도와주는 기술을 고안하는 것이 중요하다.
'연구실 > 퍼징' 카테고리의 다른 글
| [Fuzzing] Lecture 2. Lexical Fuzzing : Mutation Analysis (0) | 2024.08.22 |
|---|---|
| [Fuzzing] Lecture 2. Lexical Fuzzing : Mutation-Based Fuzzing (0) | 2024.08.04 |
| [Fuzzing] Lecture 2. Lexical Fuzzing - Code Coverage (0) | 2024.08.02 |
| [Fuzzing] Lecture 2. Lexical Fuzzing(Breaking Things with Random Inputs) (1) | 2024.07.12 |
| [Fuzzing] Lecture 1. Whetting your appetite (Exercise) (2) | 2024.07.08 |



