Exercise 1 . Testing Shellsort
def shellsort(elems):
sorted_elems = elems.copy()
gaps = [701, 301, 132, 57, 23, 10, 4, 1]
for gap in gaps:
for i in range(gap, len(sorted_elems)):
temp = sorted_elems[i]
j = i
while j >= gap and sorted_elems[j-gap] > temp:
sorted_elems[j] = sorted_elems[j-gap]
j -= gap
sorted_elems[j] = temp
return sorted_elems
우선, 예제 코드를 해석해보자.
shell 정렬 알고리즘으로 보인다. 이는 삽입 정렬의 일반화된 버전으로, 간격(gap)을 사용하여 요소를 비교하고 교환하는 과정에서 점진적으로 간격을 줄여가며 정렬을 수행하는 알고리즘이다.
아래 예시로 코드를 이해해보자.
shellsort([3,2,1])
gap = 701 일 때, sorted_elems 리스트의 길이가 3인데, gap 이보다 크므로 pass!
마찬가지로, gap 이 301, 132, ... , 4 일 때까지는 gap > 3이므로 모두 pass이다.
이제, gap = 1 일 때만 확인하면 된다.
반복문에서 i가 가질 수 있는 값은 1,2 이다
i = 1일 때, temp = 2, j=1 인데, 1>=1 & sorted_elems[0] > temp 이므로 모두 true 이다.
sorted_elems[1] = sorted_elems[0] = 3 이고, j = 1-1 = 0 인데,
0>=1 & (false) 이므로 sorted_elems[0] =temp = 2 이므로 sorted_elems = [2 3 1] 이다.
i = 2일 때, temp = 1, j= 2 인데, 2>=1 & sorted_elems[1] > temp 이므로 모두 true 이다.
sorted_elems[2] = sorted_elems[1] = 3 이므로 sorted_elems = [2 3 3] 이고, j = 1 인데,
1>=1 & sorted_elems[0] > temp 이므로 모두 true 이다.
sorted_elems[1] = sorted_elems[0] = 2 이므로 sorted_elems = [2 2 3] 이고, j = 0 인데,
0>=1 & (false) 이므로 sorted_elems[0] = temp = 1 이므로 sorted_elems = [1 2 3] 이다.
반복문이 종료되고, sorted_elems 리스트가 return된다.
따라서, shellsort([3,2,1]) == [1,2,3] 이다.
첫번째로, shellsort()가 실제로 잘 작동하는 예시로 test 해보자.
shellsort([3,2,1])
결과가 생각한 대로 잘 나왔음을 확인할 수 있다.
이제, 다양한 input들로 shellsort()를 완전히 test 해야 한다.
Part 1 : Manual Test Cases
manually하게 쓰여진 test 경우들의 숫자로 assert 문을 설정하고, 극단의 case 가 포함되는 test case 를 선택해야 한다. 두 개의 list를 비교하기 위해서 == 를 사용하자.
일반적인 경우를 살펴보자.
# Standard Lists
assert shellsort([3,2,1]) == [1,2,3]
assert shellsort([1,2,3,4]) == [1,2,3,4]
assert shellsort([6,5]) == [5,6]
exception이 발생하지 않았으므로 모든 statement 가 true 임을 확인할 수 있다.
이번에는, 리스트의 원소가 겹치는 경우를 살펴보자.
# check for duplicates
assert shellsort([2,2,1]) == [1,2,2]
마찬가지로, statement 가 true 임을 확인할 수 있다.
빈 리스트의 경우를 살펴보자.
# Empty list
assert shellsort([]) == []
마찬가지로, statement 가 true 임을 확인할 수 있다.
Part 2. Random Inputs
다음으로, shellsort()의 input 매개변수로 random한 list를 만들어보자.
우선, input list가 정렬이 되었는지 확인하기 위한 is_sorted() funciton을 구현해보자.
def is_sorted(elems):
return all(elems[i] <= elems[i+1] for i in range(len(elems)-1))
print(is_sorted([3,5,9]))
또한, 원래 리스트의 순서만 바뀐 리스트인지 확인하기 위한 is_permutation() function을 구현해보자.
def is_permutation(a,b):
return len(a) == len(b) and all(a.count(elem) == b.count(elem) for elem in a)
random list 생성자로 시작하고, [] 를 빈 list로 사용하고, 원소 x를 elems list에 추가하기 위해 elems.append(x)를 사용할 수 있다. result를 평가하기 위해 위의 helper function을 사용하자. 1000개의 list를 만들고 이를 test하자.
import random
def random_list():
length = random.randint(1,10)
elems = []
for i in range(length):
elems.append(random.randint(0,100))
return elems이는 1에서 10까지의 랜덤한 길이의 list이고, 이 list의 원소는 0에서 100까지의 랜덤한 int 값이다.
elems = random_list()
sorted_elems = shellsort(elems)
print(elems)
print(sorted_elems)
assert is_sorted(sorted_elems) and is_permutation(sorted_elems, elems)
sorted_elems 리스트는 오름 차순이고, elems의 permutation list 이다.
즉, sorted_elems는 elems의 오름 차순으로 정렬된 list 임을 알 수 있다.
for i in range(1000):
elems = random_list()
sorted_elems = shellsort(elems)
assert is_sorted(sorted_elems) and is_permutation(sorted_elems, elems)
1000개의 test case에 대해서 shellsort는 elems 리스트를 오름차순으로 정렬하는 function임을 확인할 수 있다.
Exercise 2 . Quadratic Solver
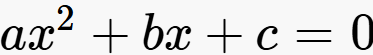
위와 같은 방정식이 주어질 때, x의 해를 근의 공식을 이용하면 a, b, c로 이루어진 식으로 표현할 수 있다.
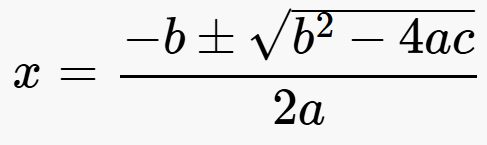
우리는 a, b, c가 주어지면, 이에 해당하는 2차 방정식의 해를 구하고자 한다.
이를 코드로 표현해보자.
def quadratic_solver(a,b,c):
q = b*b - 4*a*c
solution_1 = (-b + my_sqrt_fixed(q)) / (2*a)
solution_2 = (-b - my_sqrt_fixed(q)) / (2*a)
return (solution_1, solution_2)quadratic_solver(3,4,1)
하지만, 위의 implementation은 불완전하다. 다음 2가지를 고려해야 한다.
- ZeroDivisionException
- my_sqrt_fixed() 의 전제조건 위반
위의 2가지 경우에 대해서 error를 어떻게 방지할 수 있을까? 아래 3가지 part 를 살펴보자.
Part 1: Find bug-triggering inputs
위의 2가지 경우에 대해서 bug를 발생시키는 a, b, c에 대한 value를 확인하자.
with ExpectError():
print(quadratic_solver(3,2,1))with ExpectError():
print(quadratic_solver(0,0,1))
둘다, 근이 존재하지 않기 때문에 error 가 발생했다.
Part 2: Fix the Problem
이 case들을 적절하게 handling하기 위해서 code를 확장해보자. 존재하지 않는 value에 대해서는 None을 return한다.
def quadratic_solver_fixed(a, b, c):
if a == 0:
if b == 0:
if c == 0:
# Actually, any value of x
return (0, None)
else :
# No value of x can satisfy c = 0
return (None, None)
else :
return (-c / b, None)
q = b*b - 4*a*c
if (q<0) :
return (None, None)
if (q == 0) :
solution = -b / 2 * a
return (solution, None)
solution_1 = (-b + my_sqrt_fixed(q)) / (2*a)
solution_2 = (-b - my_sqrt_fixed(q)) / (2*a)
return (solution_1, solution_2)
print(quadratic_solver_fixed(3,2,1))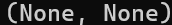
print(quadratic_solver_fixed(0,0,1))
Part 3 : Odds and Ends
random input 으로 앞서 봤던 조건을 발견할 가능성는 얼마나 될까?
1초당 10억개의 test를 한다고 가정할 때, bug가 일어날 때까지 평균적으로 얼마나 오랫동안 기다려야 하는지를 살펴보자.
def quadratic_solver_fixed(a, b, c):
if a == 0:
if b == 0:
if c == 0:
# Actually, any value of x
return (0, None)
else :
# No value of x can satisfy c = 0
return (None, None)
else :
return (-c / b, None)
q = b*b - 4*a*c
if (q<0) :
return (None, None)
if (q == 0) :
solution = -b / 2 * a
return (solution, None)
solution_1 = (-b + my_sqrt_fixed(q)) / (2*a)
solution_2 = (-b - my_sqrt_fixed(q)) / (2*a)
return (solution_1, solution_2)
위의 코드를 고려해보면, 만약 우리가 32 bit의 int형인 a,b,c의 전체 범위를 선택한다면, 첫번째 조건(a==0)을 만족하는 경우는 하나밖에 없다.
a,b 모두가 0일 가능성 p = 1 / (2^(32)∗2^(32)) 즉, 18.4 x 10^(18) 가지 중에 하나 이다.
그렇다면 1초에 10억개(10^(9))를 test할 수 있을 때, 아래 코드에 따르면 584년을 기다려야 함을 알 수 있다.
tests_per_second = 1000000000
seconds_per_year = 60 * 60 * 24 * 365.25
tests_per_year = tests_per_second * seconds_per_year
combinations / tests_per_year
즉, ramdom input에 대해서 평균적으로 584년이 지나야 조건식에 들어갈 수 있다는 것이고, 그래서 순수 random input이실제로는 testing 전략에서 충분하지 않다.
'연구실 > 퍼징' 카테고리의 다른 글
| [Fuzzing] Lecture 2. Lexical Fuzzing : Mutation Analysis (0) | 2024.08.22 |
|---|---|
| [Fuzzing] Lecture 2. Lexical Fuzzing : Mutation-Based Fuzzing (0) | 2024.08.04 |
| [Fuzzing] Lecture 2. Lexical Fuzzing - Code Coverage (0) | 2024.08.02 |
| [Fuzzing] Lecture 2. Lexical Fuzzing(Breaking Things with Random Inputs) (1) | 2024.07.12 |
| [Fuzzing] Lecture 1. Whetting Your Appetite (0) | 2024.07.03 |


